BTC比特幣為什么是2100萬枚?為什么比特幣只有2140萬枚?比特幣為什么最多2100萬?雖然網上有很多關于解說比特幣只有2100萬枚的事情,但是看完這篇文章,感覺認知更加清晰!

一片花飛減卻春,風飄萬點正愁人;
且看欲盡花經眼,莫厭傷多酒入唇。
五月的加密市場,BTC(比特幣)在6萬刀踟躕不前,春去花落一片紅。無甚熱鬧,但徜徉湖邊,看綠水青山,心底寧靜,倉位致遠。
BTC乃加密行業之根。總量2100萬之上限,乃BTC之本。一切都從這個神奇的數字展開。可是它,為何是這樣一個數字呢?
教鏈在2020年12月5日文章為什么比特幣最多只會有2100萬枚?中,就曾介紹過這個數字的計算方法。簡而言之是這樣的:

1. 每區塊產量 50 BTC
2. 每21萬個區塊,產量減半
使用等比數列求和可以輕松算出,最終BTC的總產量為:(50 + 25 + 12.5 + 6.25 + 3.125 + ...) x 21萬 = 2100萬枚。
進一步的,調節“挖礦”難度使得大約每10分鐘產生一個新區塊,即每小時6個新區塊,21萬個區塊就大概是人間4年。
這也就是比特幣4年產量減半周期的來歷。
但是,如此只是對既定事實的一個鋪敘而已。一是缺乏一些細節的考察;二是并未真正揭示比特幣發明人中本聰為何要選擇和設計這樣一個數字的原因。

首先,
2100萬并非2100萬,而是2,099,999,997,690,000。對,后面這個數字比2100萬要大1億倍,即大約是2100萬億。在比特幣系統內部,都是這個萬億級的整數。
當我們把BTC“展示”為這個整數點上8位小數位,也就變成了2 0,99 9,99 9.97 690 000。這里我用空格提示了上面作為整數時的千分位分割點。我們一眼就會看到,中本聰選擇8位小數位其實有些奇怪的,因為這樣會導致8位小數的BTC整數部分的逗號分割點,和系統內真正的整數的逗號分割點不一致。
8位小數位,也就是1億分之一,這個就不太西方。眾所周知,英文里對數字采用千分位分割,所以計數法的單位是千(thousand)、百萬(million)、十億(billion)、萬億(trillion)。英文里并沒有“億”這個單位。而中國的計數法略有不同,是以4位數字也就是萬分位為分割的,乃有萬、億、萬億。
2100萬億用萬分位分割就是這樣的:2099 9999 9769 0000;2100萬帶8位小數則是這樣的:2099 9999.9769 0000。都是4小節,每小節4位數字,沒有任何混亂。所以看起來,8位小數位,1億分之一,嗯,這很東方。
其次,
2100萬億之所以是2,099,999,997,690,000而不是精確的2,100,000,000,000,000,也正是因為8位小數位的精度限制。
上文的等比數列(50 + 25 + 12.5 + 6.25 + 3.125 + ...)并非真正的無窮數列,而是當它減小到0.0000 0001之后,再減半就歸零了。因此,這是一個截斷了的有窮數列,其加和就要小于無窮數列求和的結果100。所以,乘以21萬之后,最終結果也要略小于2100萬。
第三,
注意第一點的敘述,8位小數位和小數點僅僅是一個“展示”層面的設計。在系統內部只有那個萬億級的整數。
既然僅僅是“展示”,那么其實小數點是可以任意挪動的。現在點在8位小數的位置,以后也可以點在5位或者4位小數的位置。
比如,20,999,999,976.90000(5位小數),或者2099 9999 9769.0000(4位小數)。
那么,8位小數時的1枚比特幣,當移位到5位小數時,就顯示為1000,移位到4位小數時,就顯示為10000。相應的,原來的0.001或者0.0001 BTC現在就會顯示為1。
這移位的想法并非教鏈杜撰的,而是中本聰真實的想法。在2009年4月12日中本聰給Mike Hearn的回信[1]中,他這樣寫道:
原文:
"My choice for the number of coins and distribution schedule was an educated guess. It was a difficult choice, because once the network is going it's locked in and we're stuck with it. I wanted to pick something that would make prices similar to existing currencies, but without knowing the future, that's very hard. I ended up picking something in the middle. If Bitcoin remains a small niche, it'll be worth less per unit than existing currencies. If you imagine it being used for some fraction of world commerce, then there's only going to be 21 million coins for the whole world, so it would be worth much more per unit. Values are 64-bit integers with 8 decimal places, so 1 coin is represented internally as 100000000. There's plenty of granularity if typical prices become small. For example, if 0.001 is worth 1 Euro, then it might be easier to change where the decimal point is displayed, so if you had 1 Bitcoin it's now displayed as 1000, and 0.001 is displayed as 1."
翻譯:
“我對硬幣數量和發行時間表的選擇是經過深思熟慮的。這是一個艱難的選擇,因為一旦網絡開始運行,它就會被鎖定,我們就會被它困住。我想選擇一種能讓價格與現有貨幣相近的(數字),但在不知道未來的情況下,這很難做到。最后,我選擇了中間值。如果比特幣仍然是一種小眾貨幣,那么它的單位價值就會低于現有貨幣。如果你想象比特幣被用于世界商業的某個部分,那么全世界只有 2100 萬個比特幣,所以它的單位價值會更高。幣值是小數點后 8 位的 64 位整數,因此 1 枚硬幣在內部表示為 100000000。如果典型(應用場景的)價格變小,則有足夠的粒度。例如,如果 0.001 價值 1 歐元,那么改變小數點的顯示位置可能會更容易(查看和使用),所以如果你有 1 個比特幣,現在顯示為 1000,而 0.001 顯示為 1。”
有人說,對于普遍的64位計算機而言,如果我們使用64位二進制數同時表示整數和小數(又稱浮點數),那么最安全的做法是把整數限制在浮點數的整數部分可表達的上限內。
稍微了解計算機原理的朋友都知道,計算機內部并沒有什么小數,都是0和1的數位。所謂64位整數,就是指64個0或者1所組成的二進制整數。對應10進制就是2^64 = 18446744073709551616。這個數字要遠大于2100萬億。但是,如果要讓計算機能夠處理浮點數,那么就要把64位中拆出一部分用來表達小數部分,還要留出1位來表示正負號。這就成了IEEE 754浮點數編碼標準。其中標準定義,雙精度浮點數用64位二進制是這樣編碼的:
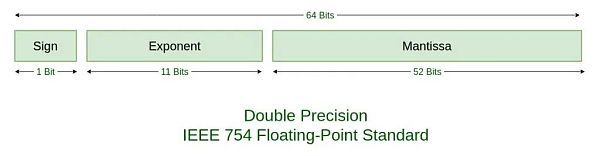
這樣一來,整數部分就只能使用53位,也就是最大不超過2^53 = 9007199254740992。而如果希望容易測試結果是否為整數,則最好不要超過2^51 = 2251799813685248。如此,可以選擇22(百萬億),但是22不是一個“三角數”(triangular number),所以中本聰選擇了21(百萬億)。

據此許多人認為中本聰選擇2100萬億,大大地方便了各種編程語言處理比特幣數量相關的計算。
不過,教鏈看了中本聰的郵件后,覺得中本聰也許并沒有這么復雜的想法。或者他的確思忖過,但是并沒有講透他的全盤考慮。他只是講,也曾經考慮過其他數字,比如4200萬億,但是感覺太大了,于是就折中成了2100萬億。在2011年1月10日中本聰回復Mike Hearn的郵件[2]中,他是這樣寫的:
"It works out to an even 10 minutes per block:
21000000 / (50 BTC * 24hrs * 365days * 4years * 2) = 5.99 blocks/hour
"I fudged it to 364.58333 days/year. The halving of 50 BTC to 25 BTC is after 210000 blocks or around 3.9954 years, which is approximate anyway based on the retargeting mechanism's best effort.
"I thought about 100 BTC and 42 million, but 42 million seemed high.
"I wanted typical amounts to be in a familiar range. If you're tossing around 100000 units, it doesn't feel scarce. The brain is better able to work with numbers from 0.01 to 1000.
"If it gets really big, the decimal can move two places and cents become the new coins."
看起來,中本聰是先定了時間諸參數,而后調整區塊產量和總量,并思考多大的數字較為適合。
依中本聰的意思,大多數人手里的BTC數量最好在0.01到1000之間,不要動輒就搞個6、7位數的幣,那樣會缺乏稀缺感。
比特幣總量2100萬個,這可能是剛接觸比特幣的小白們記得最清楚,也是最迷惑的數字。中本聰沒在任何公開的言論中提到:為什么選這個數字,于是網上出現了各種各樣的猜測和邏輯推理。
網絡上有很多種猜測,有些很靠譜,有些不靠譜但很歡樂。
答案1
It's the first half of the answer: 42.
翻譯:因為21是終極答案42的一半。
(說明:英語里,2100萬表示為:21 million。所以,老外一般直接問:為啥是21。)
當然,他是開玩笑的。不過,我個人最喜歡這個猜測,這也是reddit里頂的人最多的。
這個梗來自電影銀河系漫游指南里終極答案的橋段。
直接看視頻吧(找了一圈,只有youtube上有剪輯,所以俺加了字幕搞過來):
答案2
Because we re living in the 21st century!
翻譯:因為我們生活在21世紀!
太天真,不忍吐槽。
答案3
He chose a reward scheme and 10 minute blocks. When he did the math, it came to 21 million. He didn t choose the 21 million, he just accepted the consequence of the parameters he chose.
翻譯:中本聰訂好10分鐘、50幣、4年減半的原則,結果自然出來了。他沒有選,而是接受了這個自然的結果。
這個答案也是有可能的。中本聰在比特幣中的很多選擇確實是撞大運的,但都是“基于經驗的撞大運”。
答案4
All gold mined in human history can be fit into a cube roughly 21 meters on each side.
Satoshi created bitcoin with the idea of being sort of a digital analog of gold (finite supply, mining, etc), as well as the fact that it built upon Nick Szabo s “Bit Gold” proposal, so I think that 21 million was sort of a clever nod to that.
翻譯:全世界所有黃金熔在一起,是一個邊長大約為21米的正方體。中本聰用這個概念,隱喻比特幣是一種虛擬黃金。
原來陰謀論不止中國有
答案5
I was going to say: Satoshi likes to play Vegas blackjack.
翻譯:我覺得中本聰喜歡玩21點。
上帝玩骰子么?
答案6
計算機雙精度浮點數最多存儲2^53精度的數。而比特幣按最小單位算的總精度是2^51,剛好夠用。(英文太長不貼了)
這個答案,出現在一篇很不錯的文章里中本聰的天才:比特幣以意想不到的方式躲開了一些密碼學子彈
詳細:
比特幣有爭議的屬性之一就是它的固定的供應量。當前每10分鐘又25個新的比特幣被生產出來,并且這一數字每4年減半。總的來講,不會有超過2100萬個比特幣的存在>。另一方面,每個比特幣可以被劃分成1億份(每份叫做1“聰”),如果一美分都足夠買輛車的話,用美元來交易就麻煩重重了,但比特幣就算升值到和上面假設的美元的>狀況,也不會遇到那樣的問題。
因此,總之,將永遠存在的貨幣單位的總數字是2,100,000,000,000,000,也就是2100萬億,或者說250.899。在選擇這個數值的方>面,中本聰比大多數人意識到的要幸運的多或者說聰明的多。首先,這個數字遠小于264-1,這是一臺計算機里面可以以標準整數形式存放的最大整數,超過那個值的話,>數值將像里程表那樣歸零。
其次,然而,還有一個總“聰”數要設法低于的更小的閾值:可以用浮點的格式表示的可能的最大整數。整數不是計算機可以存儲的唯一一種數字;為了處理小數,計算機>使用一種做浮點表示法的格式。浮點表示法本質上就是一個科學記數法的二進制版本。舉個例子,下面是一個在你學習物理學的時候會遇到的值:
地球的質量: 5.972 1024 kg
太陽的質量: 1.989 1030 kg
光速: 2.998 108 m/s
一光年: 9.460 1015 m
質子的質量: 1.672 10-27 kg
普朗克長度: 1.616 10-35 m
我們可以注意到,科學記數法是如何使得你可以在合理的精度下表示所有的這些數值,盡管它們的大小相差極大。浮點表示法本質上就是二進制的科學記數法;當你存儲數>字9.625的時候,你的計算機存放的是“1.001101 * 1011”(或者說,它存放的是01000000 00100011 01000000 00000000 00000000 00000000 >00000000 00000000,這是高精度序列形式的同樣一回事)。在這個高精度形式中,系數(也就是不是指數的那部分)有52位(52bits)。這意味著高精度(更加精>確的說法是“雙精度”)浮點數足以存貯高達253的數字,但不能再高了,如果超過了,你就得開始砍掉末尾的數字。比特幣的250.9這一以指數形式表現的總“聰”數,剛>好低于這個最大值。
如果我們有了整數,我們為什么還要關心浮點值呢?因為更多的高階編程語言(比如說Javascript)并不開放低階的“浮點”和“整數表示法”,而只給程序員提供“數”的>概念 當然以浮點的形式提供。如果中本聰當時選擇了2億1千萬而不是2100萬這個值的話,用很多語言里比特幣編程就會比現在要麻煩得多了。
注意,Stefan Thomas不幸的在他寫BitcoinJS的時候沒有及時留意到這個,以至于那個庫使用了一個專門的“大數big number”對象,而不是一個普通數來存儲教程輸出值;我自己分叉的的BitcoinJS(同時還加入了其他的改進)使用了普通數。
答案7
That explanation is close but not entirely compelling. IEEE double-precision floating-point format has 53 bits of significand precision, meaning it can address up to 253 1 satoshis without any rounding error. Well, that s 9,007,199,254,740,991 satoshis, which is not anywhere close to 2,100,000,000,000,000 satoshis (or even 2,099,999,997,690,000 satoshis, which is the actual asymptotic limit).
I think a much more compelling explanation is that a signed 32-bit integer can store values up to 231 1, which is 2,147,483,647. If you assume a fixed-point format with two decimal digits of fractional precision (which is typical for money), then a signed 32-bit integer can address up to 21,474,836.47 bitcoins, which we might as well round off to 21 million. My guess is that Satoshi derived the 21-million limit from here early in development and then later realized that this wouldn t be enough currency units and so extended the number of decimal places from 2 to 8 and changed the variables from 32-bit to 64-bit.
翻譯:答案6的解釋很接近,但有點牽強。IEEE雙精度浮點數是53bits,能表示的最大數是9,007,199,254,740,991聰,而比特幣是2,099,999,997,690,000聰,差別還是很大的。
我覺得更好的解釋:有符號32位整數可存儲最大2^32-1的數,是2,147,483,647。如果比特幣是小數點后兩位的話,就是21,474,836.47個比特幣。也就是21-million。我猜中本聰在最初開發的時候用32位精度的整數,后來發現對于一種全球通用貨幣來說這個精度不夠,所以把小數點后2位延展成8位,從32位存儲改成64位存儲。
這是我覺得最靠譜的答案,因為從中本聰的過往言論可以看出,他不是一個完美主義者,而是一個實用主義者。
研究比特幣技術原理,是深入了解比特幣的最佳途徑,也是推動比特幣行業發展的基石。希望國內有更多專業的開發、技術專家進入這個領域。還有,炒幣雖爽,盯盤傷身,切記切記!
120999999.97690000
最終產生的比特幣數量,準確的說是20999999.97690000個,比2100萬少一點。
比特幣產生的時間表:
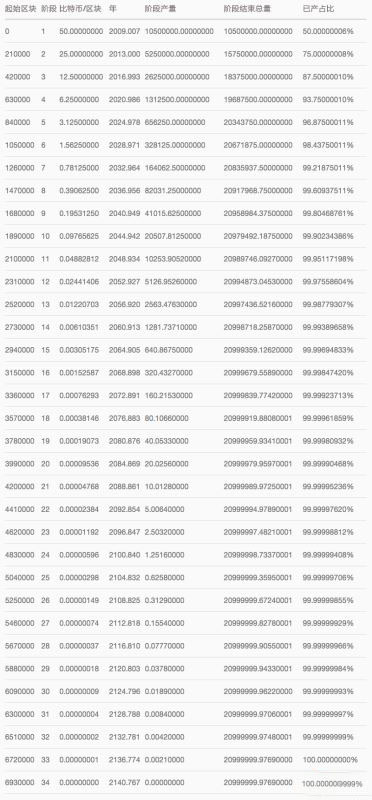
下面挑幾個重點分析一下這張表。
250.00000000
格林威治時間2009年1月3日18:15:05,創世區塊誕生。創世區塊的編號是0。從創世區塊開始的”階段1”,每個區塊產生50個新的比特幣或者說50億聰。
創世區塊:https://blockchain.info/block-height/0
3目標高度210000
格林威治時間2012年11月28日15:24:38,編號第210000個區塊產生。從這個區塊起的”階段2”,每個區塊包含的新比特幣數量減半為25個,這是歷史上第一次減半。今后每產生210000個區塊,比特幣數量都會依次減半。直到第33次減半時,每個塊產生0.0021個新比特幣直接減為0個。
210000塊:https://blockchain.info/block-height/210000
44年1次的約定
每4年減半是不太嚴格的說法。實際情況:比特幣大約每10分鐘產生一個區塊,而210000個10分鐘接近4年(4年等于210384個10分鐘。這應該是中本聰特意選取的數字)。
52016前,2016后
2016年將發生第二次減半,但現在討論這個有點早。我要說的是2016個塊的問題。
比特幣系統調節挖礦難度的原理是:根據前2016個塊產生的總時間,調整后2016個塊的挖礦難度,讓挖出這2016個塊的時間為14天。因為,每小時6個10分鐘乘以24小時再乘以14天=2016。所以,所謂10分鐘只是平均值目標。由于目前算力上漲很快,實際上挖出2016個塊的速度往往少于14天。
難度調整的話題涉及到挖礦,以后再一并分析。

上一篇:什么是芯鏈
相關閱讀推薦
最新資訊
最新游戲

史小坑的黑暗料理
查看
劍嘯江湖國際版
查看
狂飆飛車官方版 安卓版v1.0.1
查看
我的世界僵尸生存戰爭
查看
龍與家園時光(附兌換碼)
查看
紐約俠盜
查看
鋼鐵命令將軍的榮耀3
查看
末日希望
查看
盾墻游戲下載安裝正版
查看熱門文章